It would be hard to say that we are used to a drawing system by now, but in a way, yes, it is possible to get used to the attitudes or at least the on-screen requirements for Bézier manipulating (and taming) curves in order to achieve an imagined result.

Considering the examples of drawing methods we discussed so far, we know that first anchoring points are placed, and then by adjusting the control handles, the spline passing through the anchor point is dealt with. The expected attitude is one of semi-fluidity. A direction is given to the line, and we just need to adjust its swiftness and acuteness.

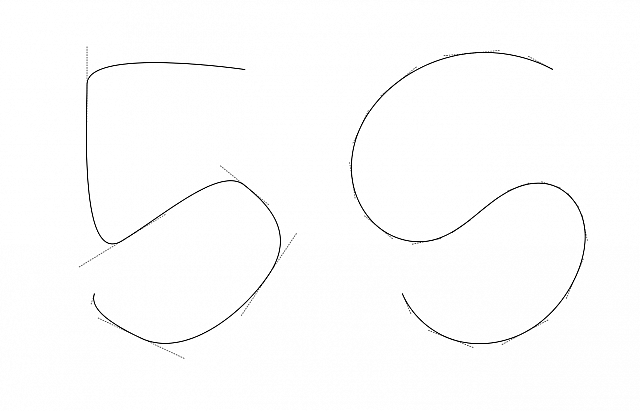
Drawing an S in Inkscape. Left showing the one using Bézier curves and right the Spiro version

How about something different though? Why must we assume that, if no overwriting properties are applied, a line that connects two anchor points, is actually straight? According to Raph Levien, this does not have to be the case. Spiro, the toolkit for curve design that he developed, starts from a totally different set of presumptions and expectations.

When drawing with Spiro, all of your lines are curved. Simply put, the structure of the line description is based on a mathematical constant. This constant describes a regular spiral. Anchor points on a Spiro curve pinpoint two locations on the progression of the spiral, be it spiraling positively, or negatively (we could say, spiraling inwards and outwards or bigger and smaller). The anchors can be attributed attitudes, not dissimilar to Bézier, but working in a totally different frame. While your control handles can influence growth or size of the spiral (your line), it retains it's curved nature.

The result is one of organicity, of fluidity, or even maybe a certain regularity. The lettershape 'S' is a useful example of a situation where you would like the curve you're drawing to understand that, by nature, it spirals, it curls, it curves and swerves. Giving an upright and proper attitude to an S lettershape is really helped by the functions of Spiro, which gives us situations of lesser amounts of control points for a shape that typically is very hard to get right.

In the 2007 post to Typophile, Raph Levien¹ wrote:

Because I'm starting at Google in a couple weeks, I won't be beating the bushes myself to push this technology out into the world. To a large extent, I'm "throwing the technology over the fence".²

In 2018, after the Google episode, Raph is back with a new spline (and a permissive MIT licence for it, and for Spiro).

One of the biggest problems with Spiro was that the underlying constraint system didn’t always have a unique solution. The solver would often fail to converge, making wild patterns reminiscent of particle accelerator tracks. That didn’t give the impression of a reliable tool; it felt like a rough research prototype. The new spline solves this problem, smoothly going through cusps in the cases where Spiro would suddenly reverse the direction of loops. I was inspired by κ-Curves, the technology underlying the new “curvature tool” in Adobe Illustrator, which also uses cusps to achieve robustness (and, kindly enough, cites my work as an example of the problem it solves). The exact approach I used was more similar to [Hobby’s splines], originally designed for Metafont, and also uses cubic segments that somewhat approximate Euler spirals as the basic curve family."³

Drawing an S with the new spline online demo tool, available on https://spline.technology/demo/

Raph Levien seems quite focused on the ease in the learning of the curve, based on the main current one. And probably

The new control is intuitive and will be familiar to designers experienced in Bézier drawing.⁴ [...] a yet-to-be-named new spline, which is another word for the algorithm and math behind the bending of a curve. This new spline will be less expressive and easier to learn (compared to the famous bezier curve) and less “wild” (compared to the spiro curve).⁵

Participants to online discussions are sometimes more interested in the very qualities of the drawing resulting of the usage of the curve.

I tried the demo and I think like I almost like the original Spiro curves a lot more. When I use your spiro curves in the inkscape, they beautifully adjust along the whole spline trying to form a curve that neatly goes through every point. These new curves do not do that, they feel and look more like your usual bezier curves.⁶

Spiro seems to represent a position at a distance from the bezier approach. Even if alternatives are developping in the space between, it's important (but also joyful) to be able to taste different flavors of curve bending to consider the very quality of the behavior of each of them.

More than a year later, a new version further tightens the combination of spiro curve tension qualities and the level of control of the classic Bezier curves. Try it out on the online version and read detailed explanations.

Diversity seems important, also in the curve arsenal.